Kumpulan Latihan Soal Beserta Jawaban Aljabar Matriks
Latihan
Soal Operasi Dasar Matriks
1. Perhatikan matriks berikut!
Tentukan
a.
2A
b.
(-1)B
c.
1/3C
d.
A + 2B
e.
A – 2B
Penyelesaian
a. 2A
b. (-1)B
c. 1/3C
d. A + 2B
e. A – 2B
2.
Perhatikan
matriks D, E, F
Tentukan
a.
DE
b.
EF
c.
(DE)F
d.
D(EF)
Penyelesaian
a. DE
b. EF
c. (DE)F
d. D(EF)
3. Perhatikan matriks G, H, I
Tentukan
a.
HI
b.
GI
c.
(GH)I
Penyelesaian
a. HI
b. GI
Karena kolom kolom matriks G dan baris matriks I tidak sama, sehingga kedua matriks tidak dapat dikalikan
c. (GH)I
4. Misalkan A,
B, C, D dan E adalah matriks-matriks dengan ukuran
sebagai berikut!
|
|
A |
B |
C |
D |
E |
|
|
|
|
(4 × 5) |
(4 × 5) |
(5 × 2) |
(4 × 2) |
(5 × 4) |
|
|
Tentukan apakah pernyataan-pernyataan matriks
berikut ini dapat didefinisikan. Bagi yang dapat didefinisikan, berikut ukuran
matriks hasilnya!
|
a. BA b. AC + D c. AE + E d. AB + B e. AB - A |
f. E(A + B) g. E(A - B) h. E(AC) i. AB j. AC(E) |
Penyelesaian
a.
BA = (4 × 5)(4 × 5)
Karena kolom matriks B
tidak sama dengan baris matriks A. Sehingga kedua matriks tidak dapat dikalikan
atau tidak dapat dioperasikan.
b.
AC + D = (4 × 5)(5 × 2) +
(4 × 2) = (4 × 2) + (4 × 2) = (4 × 2)
c.
AE + E = (4 × 5)(5 × 4) +
(5 × 4) = (4 × 4) + (5 × 4)
Karena ukuran matriks AE
tidak sama dengan ukuran matriks E. Sehingga kedua matriks tidak dapat
dijumlahkan atau tidak dapat dioperasikan.
d.
AB + B = (4 × 5)(4 × 5) +
(4 × 5)
Karena kolom matriks A
tidak sama dengan baris matriks B. Sehingga kedua matriks tidak
dapat dikalikan atau tidak dapat dioperasikan.
e.
AB – A = (4 × 5)(4 × 5) –
(4 × 5)
Sama seperti poin (d),
karena kolom matriks A tidak sama dengan baris matriks B.
Sehingga kedua matriks tidak dapat dikalikan atau tidak dapat dioperasikan.
f.
E(A
+ B) = (5 × 4)((4 × 5)
+ (4 × 5)) = (5 × 4)(4 × 5) = (5 × 5)
g.
E(A
– B) = (5 × 4)((4 × 5)
– (4 × 5)) = (5 × 4)(4 × 5) = (5 × 5)
h.
E(AC) = (5 × 4)((4 × 5)(5 × 2)) = (5 × 4)(4 × 2) = (5 × 2)
i.
AB = (4 × 5)(4 × 5)
Sama seperti poin a,
karena kolom matriks A tidak sama dengan baris matriks B.
Sehingga kedua matriks tidak dapat dikalikan atau tidak dapat dioperasikan.
j.
AC(E) = ((4 × 5)(5 × 2))(5 × 4) = (4 × 2)(5 × 4)
Karena kolom matriks A
tidak sama dengan baris matriks C. Sehingga kedua matriks tidak
dapat dikalikan atau tidak dapat didefinisikan
5. Perhatikan
matriks-matriks berikut ini
Hitunglah pernyataan berikut ini (jika mungkin)!
|
a. BA b. AC + D c. AE + E d. AB + B e. D + E f. D – E g. 5A |
h. -7C i. 2B - C j. 4E – 2D k. -3(D + 2E) l. A – A m. (AB)C n. A(BC) |
Penyelesaian
a. BA
Karena kolom kolom matriks B dan baris matriks A tidak sama, sehingga kedua matriks tidak dapat dioperasikan.
b. AC + D
c. AE + E
Karena
kolom kolom matriks A dan baris matriks E tidak sama, sehingga
kedua matriks tidak dapat dioperasikan.
d. AB + B
Karena
kolom kolom matriks AB dan baris matriks B tidak sama, sehingga
kedua matriks tidak dapat dioperasikan.
e. D + E
f. D – E
g. 5A
h. –7C
i. 2B – C
Karena
ukuran matriks 2B tidak sama dengan ukuran matriks C. Sehingga
kedua matriks tidak dapat dioperasikan.
j. 4E – 2D
k. – 3(D + 2E)
l. A – A
m. (AB)C
n. A(BC)
Latihan Soal Bentuk Matriks
Suppose the network of matrix algebra lecture message
deployment is sent via mobile phone from the chairman of class 21AB, M1 to his
colleague called M2, M3, M4, and M5, modeled in the following graph form
Note: The message flow in
the diagram can be represented by a matrix.
(Binary i.e. 0 and 1) A is the same as the number of
knots.
Arrange the spread of the message in the form matrix
A! Then determine whether matrix A is a diagonal matrix, triangular matrix or a
symmetric matrix!
The Answer
Our conclusion is matrix A doesn’t include a diagonal matrix, triangular matrix or symmetric matrix. Matrix a includes only square matrix shape.
Latihan Soal Determinan Matriks
1.
Jika diberikan matriks sebagai berikut
Tentukanlah det(C) yang memenuhi persamaan AC = B!
Penyelesaian
Sehingga,
c11 + 2c21
= 4
c12 +
2c22 = 1
c11 +
3c21 = 1
c12 +
3c22 = 3
Dengan menggunakan eliminasi
subtitusi
Dengan demikian, diperoleh
matriks dan det(C)
= 20 – 9 = 11
dan det(C)
= 20 – 9 = 11
2. Tentukan determinan dari matriks berikut! Apakah matriks tersebut singular?
Penyelesaian
|A| = (2)(1) – (3)(4) = 2 – 12 = –10
|B| = (–1)( –4) – (–2)( –3) = 4 – 6= –2
|C| = (10)(2) – (4)(5) = 20 – 20 = 0
|D| = [(–4)(2)(3) + (5)(4)(1) + (2)(0)(-6)] – [(2)(2)(1) + (4)(–6)(–4) + (5)(0)(3)]
=
(–24 + 20 + 0) – (4 + 96 + 0) = –4
– 100 = –104
Dengan demikian, diketahui
determinan matriks C = 0 atau singular
3. Diketahui matriks
Jika K21 = –8, maka nilai x yang memenuhi adalah
Penyelesaian
K21
= (–1)(2+1) M21
–8 = (–1)3
–8 = (–1)(2x – 4)
–8 = –2x + 4
2x = 8 + 4
2x =
12/2
2 x = 6
Sehingga, x yang memenuhi untuk K21 = –8
adalah 6
4.
Dengan
menggunakan minor dan kofaktor, tentukan determinan dari matriks-matriks
berikut ini.
Penyelesaian
=
0 (12 – 16) – 6(16 – 24) + 0(16 – 18) = 0(–4) –6(–8) + 0(–2)
= 0 – 48 + 0 = 48
det (C) = c31(M31)
– c32(M32) + c33(M33)
– c34(M34)
= 0[(1.1.3 + 3.1.1 + 1.0.2)
– (1.1.1 + 1.2.1 + 3.3.0)] – 2[(2.1.3 + 3.1.0 + 1.1.2) – (1.1.0 + 1.2.2 + 3.3.1)]
+ 1[(2.0.3 + 1.1.0 + 1.1.1) – (1.0.0 + 1.1.2 + 3.1.1)] – 0[(2.0.2 + 1.1.0 + 3.1.1)
– (3.0.0 + 1.1.2 + 2.1.1)]
= 0 –2[(6 + 0 + 2) – (0 + 4 + 9)] + 1[(0 +
0 + 1) – (0 + 2 + 3)] – 0
= –2(8 – 13) + 1(1 – 5) = –2(–5) + 1(–4) =
10 – 4 = 6
5.
Gunakan aturan Camer untuk menyelesaikan
3x1 + 2x2
+ x3 = 7
x1
– 2x2 = 7
2x1 + x2
– 2x3 = 8
a. Tentukan
bentuk matriksnya
b. Tentukan nilai 2x1 + 3x2 – x3






























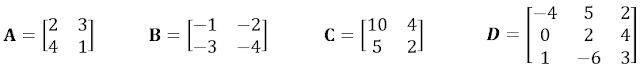











.jpeg)

Comments
Post a Comment